This problem bugs me (in a good way)
Alright let’s see.
I’ve been reading up a bit more on the ARC AGI1 problem. It’s definitely interesting.
Putting different ideas together, after reading that “Domain Specific Language” was not a novel idea (well, duh! I rarely come up with stuff nobody else has thought of, of course…), although I called it differently, a sort of “database of priors” to be mixed, in my mind, but… nevermind.
So one thing that this DSL approach reminded me is that of S-Expressions, and I had seen that as part of a variation of LCS alphabets. (see references)
Right now, RLCS only accepts binary inputs. OK, fair. What if we could encode somehow composition of functions, each one representing one prior.
After all: could it be “as simple as” encoding into binary combinations the compositions of functions?
I know I know: “If you have a hammer, everything looks like a nail”. LCS does not need to be a good approach. But… What if it was?
The idea, as-is right now…
Let’s see.
The DSL approach is really a way of talking about S-Expressions, as I understand them, from LISP.
The S-Expression mixed with LCS, I didn’t invent either, that comes from a video by Dr. Will Browne (see references).
Before I put these two things together, I basically had an idea aligned with this approach:
https://www.kaggle.com/code/michaelhodel/program-synthesis-starter-notebook
But that’s only part of it now. See, even if I were to code a huge list of priors like that, how would a program know how to combine these?
The basic DSL approach would be a brute-force attack. That wouldn’t scale and seems too… Simplistic. Basically because each “prior function” added to the list would mean checking all possible combinations again, but with one more dimension. Actually, it’s bad, because that’s exponential… Heck! What if priors application order is also relevant? And composition depth also definitely is relevant.
So I need to be able to filter (cleverly) them, somehow.
Note: I am currently also thinking about grouping: say bits dedicated for grid format, bits dedicated for color-related stuff, bits dedicated for shapes detection…
And then bits for combinations of the above, thinking here about “epistasis”. That, and what Dr. Browne calls “Code Fragments”.
I won’t go into details here, as I still am not even clear on these anyway. Maybe some other time. But there is to me a clear relation between these ideas and the ARC AGI 1 challenge.
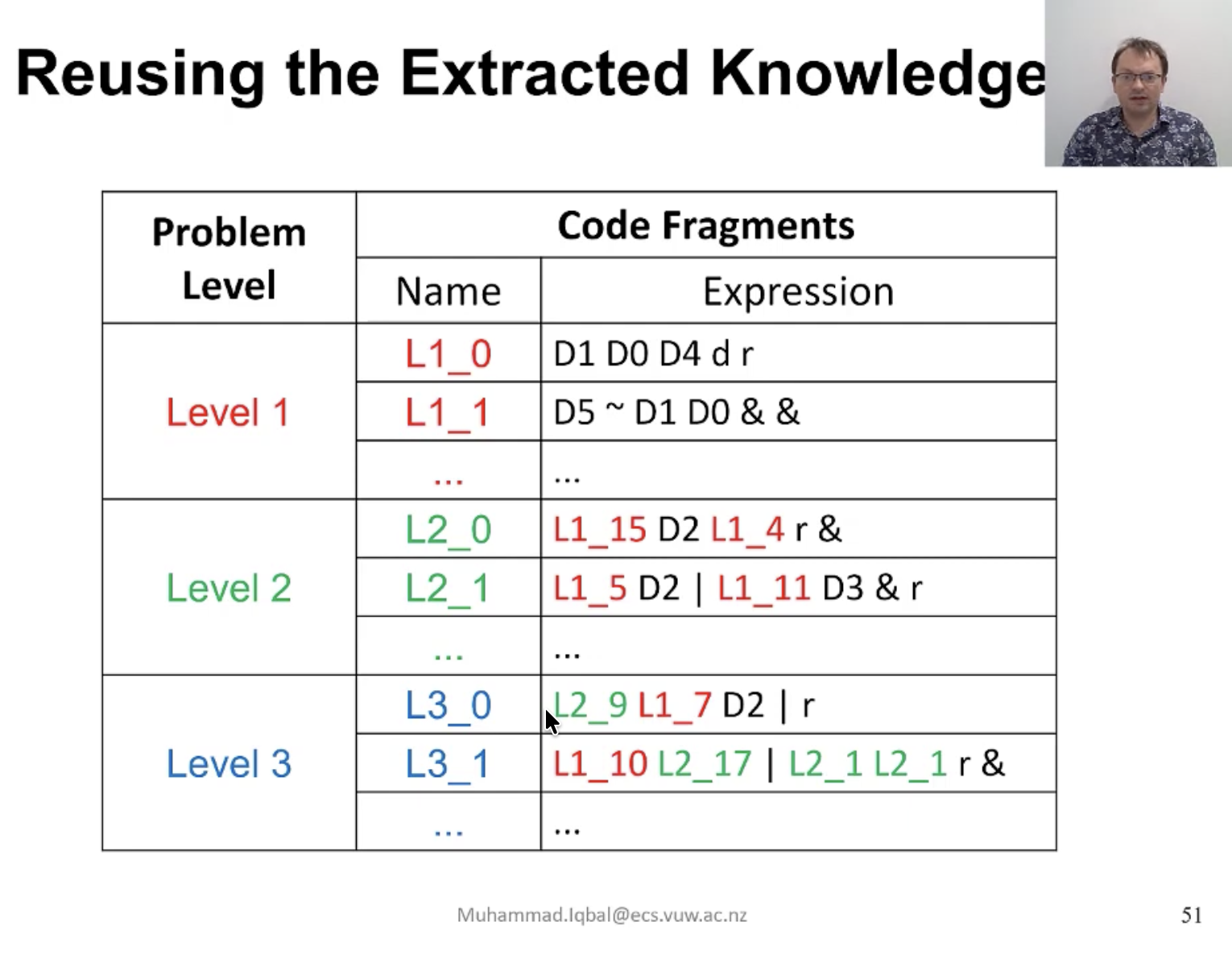
I’m actually thinking of “composing LCSs”, really.
I’ve tried something like that with Supervised Learning:
I had long search space binary strings. What I did was (and that’s not a valid theoretical approach!) split the input strings in 2, or 3, or 4 substrings… And treat each substring as an input to a simpler LCS.
IF I was very lucky, a substring would suffice to identify uniquely a solution, and then combinations of results of sub-LCSs would point to that fact.
The example was simple: “Not Bit 4” is a rather simple rule to learn, for 5 bits strings. Brute-force for instance is not out of the question (32 bit combinations).
But for 10 bits strings (1024 bits combinations), you have a larger search space to test before you come up with a result. Now, again, not correct, but the idea was:
What if I split the input strings? 5-first bits, and 5-last bits.
Then train two LCSs, one on each substrings sets (with their class of course).
Then combine the results.
You would see that 5-first bits was a sufficient sub-problem, and then result in a second layer LCS saying:
“If First Layer LCS says 1, final recommendation is 1”
“If First Layer LCS says 0, final recommendation is 0”
“Disregard completely second Layer LCS”
Training each sub-LCS was way faster, of course, as the search space is much reduced.
That’s just an idea, but I think it’s hinting at what could be a valid approach, if I can reduce ARCAGI1 problems to sub-groups…
And conceptually, I would have implemented right there a sort of compounded LCS, multi-layer LCS of sorts, and that would in fact be similar to breaking large problems in sub-problems and then combining them, and somehow that’s… What I currently understand of the S-Expression approach, “Code Fragments”, or whatever you want to call them.
Then if I encoded each “sub-LCS” as one unique problem solution… Could I then test multiple-level such combinations, choosing each encoded unique sub-problem (that can be a binary string, right there…)?
Oh! One more thing! So to choose a combination of priors for any one given example, I should of course consider some error distance. That’s kind of obvious, sure, but still!
That’s where I’m at right now.
Conclusions
Well, for now: A database of “priors”, and a sort of variation on “Code Fragments”. And then apply LCS to training examples, to come up with “composed code-fragments” that are more useful.
I feel encoding of input will be key. I don’t see why I couldn’t use the ternary alphabet still, if I somehow encode combinations and rules separately. Each “code fragment” (in the terms of the referenced videos) I would encode with a dedicated number. Then a number is just that, a number, so it can still be easily encoded as binary code. IDK.
You could then put fragments in order and try to apply them. First (or last?) bits of the input would be application orders.
After training some combinations would stand out? That would help prioritize testing combinations, effectively somewhat pruning the search space which could be huge…
But clearly, I don’t know. It’s just very interesting.
References
I will have to keep digging. Here a few options to review…
Some of Dr. Will Browne’s videos are very helpful for me to think about approaches…
https://www.youtube.com/watch?v=fN1Fkbx3TnU <- This video is packed with interesting ideas…